How to Find the Area of a Triangle

August 26, 2023

Are you looking for the area of a triangle? Well, that’s easy to find. Triangles are basic geometric shapes that appear in various fields of mathematics, science, and everyday life.

From architecture and engineering to art and navigation, the concept of calculating the area of a triangle holds universal significance. Whether you’re solving practical problems or delving into abstract mathematical concepts, understanding how to find the area of a triangle is an essential skill.

This guide aims to provide a comprehensive introduction to the methods and formulas used to find and determine the area of triangles.

What Is The Area of a Triangle?

The area of a triangle refers to the space enclosed by the lines that make up its sides. This area can vary between different triangles based on factors such as the lengths of the sides and the angles between them.

To measure the area of a triangle, we use units like square meters (m²), square centimetres (cm²), or square inches (in²).

Definition of a Triangle

A triangle is a closed shape with three corners, three sides, and three angles. It’s a basic geometric shape represented by the symbol △. Triangles come in various types, each distinguished by the lengths of their sides and the sizes of their angles.

Common Types of Triangles

Triangles are classified based on their sides and angles. Here are the three main types of triangles:

Equilateral Triangle

In an equilateral triangle, all three sides are of equal length, and all three angles are equal, each measuring 60 degrees. Equilateral triangles are symmetrical and have a balanced appearance.

Isosceles Triangle

An isosceles triangle has two sides that are the same length, and two angles that are the same. The angles that are across from the equal sides are identical to each other. The third angle, opposite the base, is typically different from the other two angles.

Scalene Triangle

In a scalene triangle, each of the three sides has a different length, and all three angles are distinct from each other. Scalene triangles are the most irregular type of triangles and do not possess any equal sides or angles.

It’s also worth mentioning some special cases:

Right Triangle: A right triangle has one angle measuring 90 degrees (a right angle). The side opposite the right angle is called the hypotenuse, while the other two sides are the legs.
Obtuse Triangle: An obtuse triangle has one angle greater than 90 degrees (an obtuse angle).
Acute Triangle: An acute triangle is a type of triangle where all three angles are smaller than 90 degrees.

These classifications are based on the lengths of the sides and the measures of the angles, and they provide a foundational understanding of the properties of triangles.

How To Find the Area of a Triangle

Here are simple ways to find the area of a triangle:

Using the Base and Height

Find the Base and Height: Look at the triangle and find one side that’s like the “bottom.” This is called the base. Then, imagine drawing a line from the opposite corner straight down to the base. This line’s length is the height of the triangle. Sometimes you’re given these lengths, or you can measure them yourself.
Use the Formula: The formula for the area of a triangle is: Area = (1/2) × (Base × Height). Just remember to divide by 2 after multiplying the base and height.
Calculate the Area: Put the numbers for the base and height into the formula. Multiply them together, then divide by 2.
This gives you the area of the triangle in square units.
For example, if the base is 5 cm and the height is 3 cm: Area = (1/2) × (5 × 3) Area = (1/2) × 15 Area = 7.5

So, the area of the triangle is 7.5 square centimetres.

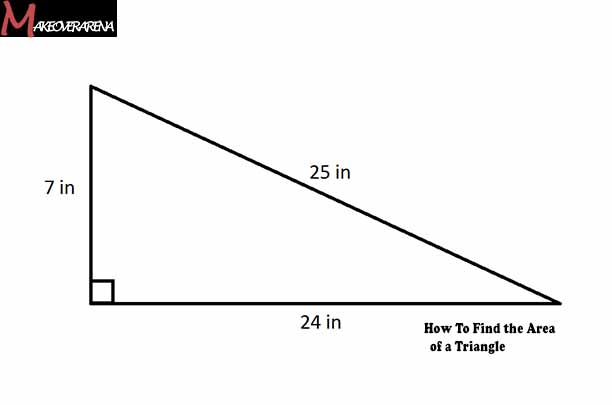
And if you’re dealing with a right triangle, you can use the same formula. Just remember, for a right triangle, one side is the base, and the other is the height.

If you know the hypotenuse (the longest side), you can use the Pythagorean Theorem to find the missing side, and then use the formula to find the area.

Using Side Lengths

Calculate Half the Perimeter: Imagine you’re finding the halfway point of walking around the edges of a triangle. This halfway point is called the “semi-perimeter.” To get it, add up the lengths of all three sides of the triangle, and then divide that total by 2. For example, if a triangle’s sides are 5 cm, 4 cm, and 3 cm long: Semi perimeter = (5 + 4 + 3) / 2 = 12 / 2 = 6
Heron’s Formula Setup: Now, set up the formula to find the area. The formula is a bit like a secret code: Area = √(s × (s – a) × (s – b) × (s – c)) Here, ‘s’ is the semi-perimeter you found, and ‘a’, ‘b’, and ‘c’ are the lengths of the triangle’s sides.
Plug in the Values: Put the semi-perimeter and the side lengths into the formula. Remember to use the semi-perimeter instead of ‘s’ in the formula.
Calculate the Values: Subtract each side length from the semi-perimeter, then multiply these three values together.
Multiply and Square Root: Multiply the result from step 4 by the semi-perimeter, then find the square root of that number. This will give you the area of the triangle in square units.

For example, if you have a semi-perimeter of 6 and side lengths of 3, 2, and 1: Area = √(6 × 3 × 2 × 1) Area = √(36) Area = 6

So, the area of the triangle is 6 square units.

Using One Side of an Equilateral Triangle

Know the Side Length: If you know the length of just one side of an equilateral triangle, you’re good to go. All sides are equal in this type of triangle.
Use the Formula: There’s a special formula for finding the area of an equilateral triangle: Area = (s² × √3) / 4. Here, ‘s’ stands for the side length you know.
Plug and Square: Put the side length into the formula, and then square it (multiply it by itself).
Multiply by √3: Multiply the squared side length by the square root of 3. You might need a calculator for this part, or you can use the rounded value of 1.732.
Divide by 4: Finally, divide the result by 4. This will give you the area of the triangle in square units.

For example, if you have an equilateral triangle with sides that are 6 cm long: Area = (6² × √3) / 4 Area = (36 × √3) / 4 Area ≈ 15.59

So, the area of the equilateral triangle with sides 6 cm long is about 15.59 square centimetres.

Using trigonometry.
Know Side Lengths and Angle: If you know the lengths of two sides of a triangle that touch at a corner, and you also know the angle between these sides, you’re set. These sides are called “adjacent” sides.
Use the Formula: There’s a special formula involving trigonometry: Area = (b * c / 2) * sin(A). Here, ‘b’ and ‘c’ are the lengths of the adjacent sides, and ‘A’ is the angle between them.
Plug and Multiply: Put the side lengths into the formula and multiply them together. Then divide the result by 2.
Find the Sine: Use a calculator to find the sine of the angle ‘A’. It’s like a button on the calculator that says “SIN”. For instance, if the angle is 123 degrees, the sine might be around 0.83867.
Multiply and Get Area: Multiply the result from Step 3 by the sine value you found in Step 4. This gives you the area of the triangle in square units.

For example, if you have two adjacent sides that are 150 cm and 231 cm long, and the angle between them is 123 degrees: Area = (150 * 231 / 2) * sin(123°) Area = (34,650 / 2) * 0.83867 Area = 17,325 * 0.83867 Area ≈ 14,530

So, the area of the triangle is about 14,530 square centimetres.

FAQ

What’s the Area of a Triangle?

The area of a triangle is the space inside the triangle formed by its three sides.

What If We Know Two Sides and the Angle Between Them?

In this case, the area equals half of those two sides multiplied by the sine of that angle.

How Do We Find the Area if we Know all Three Sides?

When we know all three sides, we can use something called Heron’s Formula to find the area. It’s a bit more advanced, and you can find more about it in the ‘Area of a Triangle by Heron’s Formula’ section in this article.

How About Using Vectors to Find the Area of a Triangle?

Imagine vectors u and v making a triangle in space. The area of this triangle is half of the size of the U cross multiplied by v. In symbols, it’s A = ½ |u × v|.

What Is the Basic Way to Calculate the Triangle Area?

If you know the base of the triangle (that’s like the bottom length) as ‘b’ and the height ‘h’, then just multiply them together and divide by 2. So, Area (A) = ½ (b × h) in square units.

CHECK THESE OUT: